Go to evaluation of the output if you need a quick help to optimally run MotifSampler.
If you have not used MotifSampler before, go through the following steps :
    Introduction
    Theoretical background of the algorithm
    Input for the algorithm
    MotifSampler Algorithm
    Output to the user
    Evaluation of the output (includes link to step-by-step approach in MotifSuite)
Optionally, also read an elaborate discussion on the results of MotifSamplers performance in a case study.
    Case study : Improved motif detection performance of MotifSampler version 3.1.5 on real benchmark datasets.
    Case study : Improved motif detection performance of MotifSampler on real benchmark datasets when using a conservation-based PSP for the detection of motifs well conserved in close orthologs.

Introduction

MotifSampler is a probabilistic de novo motif detection tool designed to search for regulatory motifs in DNA sequences upstream of coregulated genes from one species. Compared to the first release of MotifSampler (3.1.1, Thijs et al. 2002), the 3.1.5 release of MotifSampler addresses some functional bugs, offers a wider range of prior probability distributions for estimating the number of instances per sequence (parameter -p) and improves the way the information of the internally computed distribution on the number of instances in a sequence is summarized in the algorithm. The latest release (motifsuite_v2) can integrate position-specific prior (PSP) information to guide the motif search towards DNA regions that are more likely involved in active regulation.

In what follows, we give a comprehensive description of MotifSampler and we provide guidelines on selecting program parameter settings and evaluating the output. If you want to use this application, go back to the applications webpage or setup the MotifSampler commandline in case of standalone use. Note : all program parameters described below have default settings in MotifSampler unless stated otherwise.

Theoretical background of the algorithm

MotifSampler belongs to the class of probabilistic motif detection programs that typically model motifs by a PWM (Position Weight Matrix) and the remainder of the sequence by a background model. The goal of such programs is to find the motif model that differs most significantly from the background model, therefore being a candidate functional (regulatory) motif in the input sequences dataset.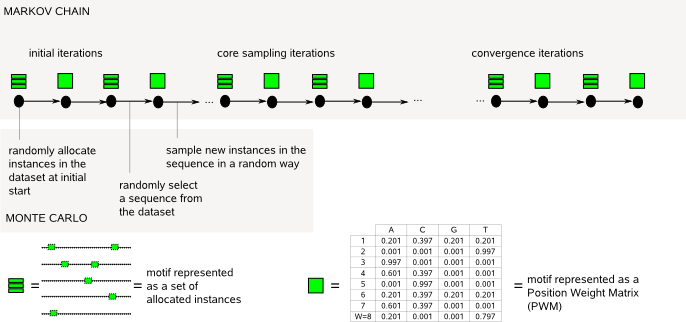

In MotifSampler, the background model is supplied by the user and the motif model is described by two variables : 1) its PWM, describing the probabilities to find the respective nucleotides A,C,G,T on each position of the motif and 2) a set of instances, being short DNA sequences annotated by their relative start positions in the input sequence set, also called predicted Transcription Factor binding sites. The algorithm in MotifSampler applies a statistical optimization technique (Gibbs sampling) to simultaneously define these two motif variables based on a Markov Chain Monte Carlo (MCMC) approach (Fig.1). MCMC means that (Markov Chain:) the results from each step depend only on the results from the preceding step and (Monte Carlo:) the way to select the next step is done in a random way.

The central idea of how this is achieved is that the more accurate the description of one variable in one step, the more accurate will be the description of the other variable in the next step. So once some true instances have been selected by chance, the PWM starts to reflect the true motif and this process tends to recruit further true instances. The selection of instances is done by random sampling from a score distribution in such way that multiple combinations of different potential instances are sufficiently explored at the same time reducing the risk to quickly converge to a suboptimal solution. Because of the random property, the reported solution by MotifSampler may be (slightly) different if you repeat the iteration process on the same input sequence set with the same MotifSampler parameter settings. A true motif, however, will have a strong signal compared to the background and will be detected multiple times when repeating MotifSampler multiple times, as can be assessed with the post processing programs (MotifRanking, FuzzyClustering) available in MotifSuite.

Input for the algorithm

- a file (parameter -f) containing a set of DNA sequences in FASTA format. MotifSampler is designed to work on a set of DNA sequences that are expected to have a set of short sequences that are more overrepresented compared to the background in which they are hidden. Such sequences are typically derived from gene expression or ChIP-based experiments.
- an optional file (parameter -q) containing a set of PSP scores in PSP format. The PSP scores reflect for each position in (one, or some, or all of) the input sequences the a priori belief this position is part of a motif. PSP scores are typically derived from experiments with evidence on the in vivo active binding such as nucleosome positioning, DNAseI hypersensitivity, ChIP-Seq peaks or other epigenetic TF binding characteristics.
The impact and how to optimally use a PSP is described in the PSP guidelines. In case you choose to use the PSP-method to preferentially search for (likely well conserved) motifs in well conserved DNA regions, you can construct a conservationPSP on your input DNA sequences using our CreateConservationPSP application.
Mark that our motif detection algorithm assumes a uniform PSP-distribution over DNA positions in sequences where no user-PSP is provided (i.e. each position is a priori equally likely/unlikely part of a motif).
- a file (parameter -b) containing a background model (format) that describes non-coding background information of the genome of interest. A higher-order background model is in general a better choice to model the background information of the sequence dataset than simple single nucleotide frequencies. We have a list of precompiled background models available for a list of pro- and eukaryotes or you can create such a model yourself using CreateBackgroundModel.

MotifSampler Algorithm

The algorithm of MotifSampler searches for one motif at a time. In its search for one motif, the algorithm is initialized by choosing exactly one instance of length w (parameter -w) at random in each sequence. It then proceeds through a sequence of (1) initialization iterations, (2) core sampling iterations to end with (3) convergence iterations (Fig.1). Each iteration in principle repeats the following two steps for every sequence in the dataset (Fig.2) :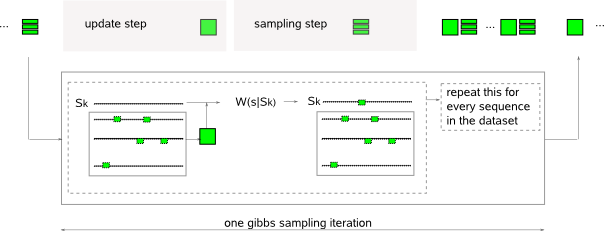

- update step : a set of instances is known at the end of the previous step. One sequence is excluded from the dataset (Sk) and a PWM is constructed based on this reduced set of instances. The reduced-PWM construction uses the nucleotide counts for A,C,G,T on each position in the reduced set of instances and a set of pseudocounts. The pseudocounts reflect a positional prior belief on A,C,G,T (derived from the PSP information if so provided in inputfile -q) and at the same time avoid the occurrence of singularities.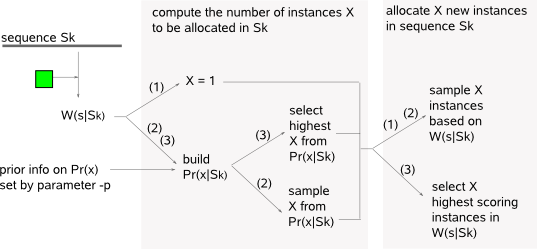
- sampling step : the PWM known at the end of the previous step is used to build a segment score distribution W(s|Sk) by computing for every possible segment of length w in sequence Sk a score that represents its probability to be a motif (as known at this stage) divided by its probability to be non-functional background. The score W(s|Sk) includes a factor representing the prior probability of this segment to be a motif or not. This factor is derived from the PSP information if so provided for sequence Sk in inputfile -q.

Fig.3 shows how the sampling step is different for the 3 types of iteration phases : In the initialization phase (1), exactly one instance is randomly sampled from the segment score distribution W(s|Sk) in sequence Sk in such way that the probability to sample a segment is proportional to its score. In phase (2), we change the number of instances to be sampled from W(s|Sk) by internally computing a distribution Pr(x|Sk) that represents the probability to have x instances in sequence Sk for every possible x from zero to a maximal number set by parameter -M. Parameter -M is supplied by the user and equals the maximal number of instances of one motif that may be allocated in each sequence of the dataset. Parameter -p describes a prior distribution Pr(x) that allows the user to bias the motif search towards a given number of instances per sequence (Pr(x) applies to every sequence in the dataset and is fixed for all iteration phases). The eventual number of instances X to be allocated in sequence Sk is sampled from Pr(x|Sk) in such way that the probability to sample X is proportional to its probability score in Pr(x|Sk). Phase (3) also considers a higher number of instances X but the random aspect of sampling from W(s|Sk) and Pr(x|Sk) is for reasons of convergence replaced by a deterministic choice of the highest scoring element(s) in the distribution at hand.

The random aspect of sampling in (1) and (2) enables the motif detector to better explore multiple possible solutions. High scoring instances have a higher probability to be sampled than low scoring instances and the closer we get to the best possible optimal solution in the dataset, the more informative will be W(s|Sk) and Pr(x|Sk) and the less likely the motif detector will iterate away from this solution. In the final phase (3), we assume that the motif detector is already near a good (hopefully the best) optimal solution in the dataset and by selecting the highest scoring values, the motif detector is guided towards the nearest optimal solution to end the detection process. The PWM and set of instances retrieved at the end of the convergence phase are the representations of 1 single candidate motif that are reported to the output files of parameter -m respectively parameter -o.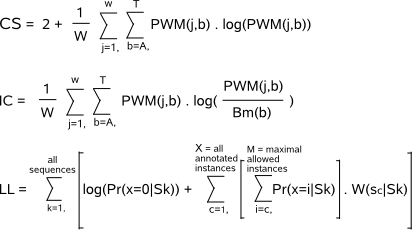
[Optional : read more on the construction of W(s|Sk) - Fig.4 and Pr(x|Sk) - Fig.5]

Parameter -s sets the strand (direction of transcription) in the sequence to search for motifs. At default 'both strands', the program will repeat the sampling step as described above on the reverse complement of each sequence, by this covering the possibility that the motif might be located on the strand opposite to the sequences'strand supplied in the input file.

In the text outputfile, MotifSampler reports a set of 3 scores (Fig.7) that each account for a specific aspect of the putative motif : consensus score (CS), information content (IC) and log-likelihood score (LL).

-CS is a measure for the conservation of the motif and this score can be used in absolute terms. A perfectly conserved motif has a score equal to 2 while a motif with a non-informative uniform nucleotide distribution has a score 0.
- IC takes not only into account how well the motif is conserved, but also how much the motif differs from the single nucleotide background distribution (#snf supplied in parameter -b). The IC score is maximal (equals 2) if the motif is well conserved and differs considerably from the background distribution.
- LL depends both on the conservation and the total number of instances of the motif. LL can thus be equally high for a well conserved motif with few instances as for a degenerate (i.e. less well conserved) motif with many instances. The absolute value of the LL score depends on the properties of both the motif and the dataset (length of the motif, number of sequences in the dataset) and should not be compared between motifs from different datasets.
Both LL and IC take into account more information on the motif than CS, but they depend on a correct description of the background model (parameter -b).

Finally, parameter -r sets the number of times the motif detection algorithm (one run) must be repeated. In MotifSampler, one run of the algorithm will perform 99 iterations, starting with 19 initializations, 70 core sampling and 10 convergence iterations and the result is one motif represented in two formats (i.e. as a set of instances annotated in the sequence dataset and as a PWM). The process of 99 iterations is repeated multiple times (default 100 runs) reporting a list of multiple solutions where the true motif(s) must be extracted from by means of a statistical assessment (with MotifRanking and/or FuzzyClustering).

Parameter -n and parameter -x are used to search for different motifs in a sequence set. When n is set higher than 1, the MCMC sequence of 99 iterations within one run is restarted n times, after each time first excluding from further allocation all segments in the sequence set that overlap more than allowed by parameter -x with the instances assigned to the previously detected motif(s) in the same run. By consequence, the motif detector is forced to find subsequent motifs that will are different from the already detected motif(s) in the same run. In MotifSampler, the different motifs detected within one run are reported one after another and their motif identifiers have the same first run-number and a different second restart-number e.g. box_1_1, box_1_2, box_1_3. The number of restarts is repeated in every run and the total number of reported putative motifs by MotifSampler now equals the product of parameter -r and parameter -n. Mark that parameter -x is not used by the program if n is lower than 2.

- Parameter -Q allows for the user to guide the motif search more or less intensely towards DNA regions that were attributed higher PSP scores in the inputfile (-q). The setting of Q is an integer non-negative number. If Q=0, the positional motif search bias is ignored. Q can be interpreted as the number of times a test (that gives evidence on a position being involved in regulation or not) was executed. The higher the number of tests, the stronger your belief in the produced prior information. By design, the motif prior belief used in our motif detection algorithm (so-called pseudocounts) always includes one test, in which we assume a uniform prior belief. This uniform prior expresses that any sequence position and any A, C, G or T are equally likely to be, or not be, part of a motif. With a low setting for Q, the impact of your non-uniform positional motif prior is minor and you allow the dataset to speak for itself during the iterative motif detection search. The higher Q (>>10), the stronger you will guide the motif search towards DNA regions with high prior regulatory evidence. Consequently, the algorithm runtime is likely to be faster.

Output to the user

The algorithm reports two files that each describe the same set of candidate motifs detected by the algorithm in a different format :
- a text file (parameter -o) reports each solution as a set of motif instances (read instances format)
- a matrix file (parameter -m) reports each solution as a Position Weight Matrix (read PWM format).
The first file additionally also reports the number of sequences where at least one instance was detected, the total number of instances and scores (CS, IC and LL) of a given detected motif.

Evaluation of the output

The number of solutions reported by MotifSampler is expected to equal the product of parameter -r and parameter -n. If there are less solutions reported, then MotifSampler did not converge to a reasonable solution (i.e. when the number of instances at the end of an iteration step is not higher than 2, the detection procedure is aborted). If the number of solutions obtained at MotifSamplers default settings is still sufficiently high to perform a proper statistical assessment (minimal 50 or 70 solutions on the safe side), we recommend to first run MotifRanking on the matrix output file (-m) to quickly see how frequently a motif was detected. If this frequency (return ratio RR) is sufficiently high (minimal 10% or 30% on the safe side), the retrieved motif can be regarded as a statistically significant solution that most likely represents a true motif. If no interesting motif was obtained, you should repeat MotifSampler with revised parameter settings (discussed below) that influence the way the motif detector walks and converges towards the most optimal solution in a dataset.

- parameter -s : Allocating instances in both strands (-s = 1) of a sequence may be more prone to picking up untrue motif instances, because the number of sequences is doubled and therefore also the signal to noise ratio is decreased. This decrease in signal to noise ratio might prohibit finding an optimal solution in one run. Resetting to single strand (-s = 0) might result in missing some true motif instances but in most cases improves the PWM representation of the true motif.

- parameter -r and -n : The search for more than 1 motif can be achieved in two ways : by increasing parameter -r (number of runs that report 1 motif) or by increasing parameter -n (number of motifs to be searched for in one run). The first way (-r) will increase the number of reported solutions linearly with the setting for -r. Many of the detected motifs will be similar (and should be similar for a solution to be statistically significant), so when different motifs have a motif signal strength of the same order, they will each be frequently visited by the motif detector and appear as different statistically significant top-ranked solutions in MotifRanking. If, however, a dataset has different motifs with a very different motif signal strength, increasing -r may only increase the detection frequency of the more conserved (easily detectable) motifs. The second method (-n) is more capable of retrieving the weaker motifs as the motif detector is forced to allocate only parts of the sequence that were not yet alloacted to previously detected motifs. A side effect is however that instances that have been wrongly assigned to a first motif are now no longer available to be assigned to a subsequent motif, increasing the risk to report a meaningless motif or no motif at all.

- parameter -b : A wrong background model may lead to high segment scores in W(s|Sk) for many factually untrue instances because they differ from the 'wrong' background. In that case, a set of multiple instances that differ considerably from the background but that show a low degree of conservation might result in a high LL score. These motif candidates are most likely false positives. We therefore recommend the use of a precompiled background model (check on our server) or a (higher-order) background model that optimally describes the composition of non-functional background for the genome of interest. Please read CreateBackgroundModel guidelines on how you can evaluate background model properties. Optionally, read article 1 and article 2 on how (genome-specific) higher-order background models can improve motif detection.

- parameter -M : This parameter sets the maximum number of instances that can be allocated in any sequence of the dataset when searching for one motif. The choice for -M is a balance between program runtime, convergence and the expected accuracy to describe the full set of true motif instances. A high value for -M means a longer runtime (i.e. the construction of the internally computed distribution on the number of instances in a sequence (Pr(x|Sk)) becomes computationally expensive for values higher than 3) and more risk that the motif detector includes untrue instances that eventually may distract the motif detector from converging towards the most optimal solution. A low value on the other hand might result in only detecting a subset of well conserved instances of the true motif or to no solution at all because the overrepresentation signal of the detected motif does not get strong enough. A good guideline is to use limited values for -M (e.g. 1 or 2) and look for more occurrences of the detected motif in a second step (e.g. run MotifLocator with the detected motif as prior on the sequence dataset or repeat MotifSampler with an increased value for -M and run MotifComparison to confirm if the detected motifs obtained at both -M settings are the same). Higher values for -M are best used in combination with a fixed distribution (e.g. -p = f0_0_0_1, see parameter -p) on datasets where each of the sequences is expected to have a high number of motif occurrences. Mark that the setting for -M should be in line with the chosen prior distribution (-p) on the number of instances per sequence (do not expect to allocate 3 instances per sequence with -M = 3 if the prior probability in -p for 3 instances per sequence is 0).

- parameter -p (read -p priors for details on possible settings for -p) :
The default prior distribution (type 1, -p 0.9_0.25) is designed to bias the search for mainly 1 instance in each sequence of the dataset, but 0 allocations (when the motif signal is weakly conserved in a sequence) or 2 allocations (when there are multiple strongly conserved motif instances in a sequence) are also possible. Use this distribution when you are interested in (quick) convergence, short runtime and detection of the core of a motif, maybe at the cost of missing some true instances. Using the PWM representation of this core motif in MotifLocator is a good strategy to further pickup true instances of the motif in a sequence set. Alternatively, you can see if you obtain the same motif when exploring prior distributions that bias towards multiple motif allocations in a sequence. The statistical significance of the obtained solution should be of the same order as for the solution detected with the first setting for -p. If lower, you have used an overestimated prior that deviates the motif detector too much from the true underlying motif signal. Priors biasing towards multiple instances are for example -p 0.9_0.75 (for mainly 1 or 2 instances per sequence) or the binomial distribution (type 3, search for multiple instances with a window of about plus or minus one instance around a mean value) such as b0.5 (search for mainly 2 or 3 instances per sequence). Or use the explicit prior distribution (type 4) when the above distributions do not meet the a priori information you want to supply to the program.
The prior distribution in parameter -p accounts for every sequence of the dataset. In real situations, datasets most likely have a variable number of instances over the different sequences. The use of an unbiased prior (the uniform prior, -p u) leaves it up to information embedded in the sequences itself to determine the number of instances in each individual sequence. When a statistically relevant solution is found, the reported motif is most likely the most accurate description of the full set of instances of a true motif that can be obtained with MotifSampler (i.e. a minimal number of untrue instances balanced with a maximal number of true motif instances). A disadvantage is a higher risk of many run abortions (making the results less suitable for statistical assessment). Nevertheless, if the number of times (absolute count) that the same motif was detected is still higher than 20 (assuming 100 initiated runs), the detected motif can still be regarded as a meaningful solution. Because the uniform prior does not guide towards a limited number of instances, you need to verify that -M is set to a reasonable limited value to control the program runtime.
When no statistically significant solution is retrieved with above settings for -p, try to detect (at least a subset of) the difficult to find motif instances by forcing MotifSampler to allocate a fixed number of instances (1 with f0_1 or 2 with f0_0_1) in each sequence in every iteration step of a run. The fixed distribution (type 5) guarantees that all runs report a solution and a fast runtime (the construction of the internally computed probability distribution Pr(x|Sk) is skipped at each Gibbs sampling iteration step). Untrue instances can be filtered out by relying only on those instances that have the highest motif instance scores in the text outputfile of MotifSampler.

In a more advanced approach, you can merge the motif detection results obtained in multiple MotifSampler trials that each time used different parameter settings and use FuzzyClustering to compose ensemble motif(s). This method is focused on extracting a maximal number of true instances from the merged solutions without reporting unreliable allocations. For cases where MotifSampler visited different but overlapping small subsets of the true motif, the result may describe the true motif signal surprisingly well.

The most appropriate setting for parameter -p is also discussed in MotifSuite's step-by-step approach.

- parameter -q and -Q : Using a positional motif prior does not necessarily lead to an improved motif detection performance if prioritized positions make up segments (potential DNA sites) that overall have a low sequence similarity. Also, positional prior motif evidence does not guarantee prioritized positions are regulated by the same motif. So unless regulatory evidence and motif specificity is very clear from a PSP-generating experiment, it is in general better to set a treshold and only retain non-zero PSP scores (in your inputfile -q) for those sequences (or even only those regions in a sequence) for which the evidence is sufficiently informative. PSP scores can then operate as the provider of essential DNA sites that serve as seeds that guide the motif search towards a particular motif. Given motif detection convergence, a high value setting for -Q will favor a higher true motif accuracy i.e. reported motif instances are supported by both sequence specificity and other concepts that play a role in active regulation.
A good guideline is to first run the MotifSampler-MotifRanking pipeline with the default Q-setting, valueing both sequence specificity (sequence conservation) as the positional motif prior as important, and set -M = maximum 1 or 2 instances per sequence. Repeating this pipeline with a higher Q (e.g. 100) is worthwhile to maybe also find less conserved true motif instances. Once a significant motif is found, use MotifComparison to see if the detected motifs are the same, or use MotifLocator to find more motif occurrences in a second step.

Feedback

Contact us if you have comments, questions or suggestions or simply want to react on the contents of this guideline. Thank you.