Introduction
    Integrate prior information in computational motif detection
    Impact of a PSP on the motif detection algorithm
    Using a PSP
    Special case: Create a conservation-based PSP

Introduction

While the present-day computational motif detection algorithms can accurately predict in vitro binding, solutions represent the in vivo reality more accurately when used in concert with additional regulatory knowledge. Integrating additional knowledge into the Gibbs sampling scheme can be challenging with computational or analytical complexities and uncontrolled outcome. Position-specific prior (PSP) information expresses a prior belief over DNA locations on how likely these positions are involved in active regulation. Using a PSP in the Bayesian framework of Gibbs sampling to guide the detection towards prioritized DNA regions is fast, easy and efficient.

We have integrated the option to use a PSP (input parameter -q and -Q) in both our motifdetectors MotifSampler and PHMS and NOMS. Especially in the latter applications, it is an interesting option to generate PSP-input on a well studied reference species to create good initialization seeds to find motifs in unexplored related species. As a special case, we present and demonstrate the use of a conservation-based PSP in MotifSampler as an elegant and effective way to detect motifs that are well conserved in close orthologs, without the need to add the orthologous sequences in the motif search.

Integrate prior information in computational motif detection

Active binding of a TF with its target TFBSs to perform a regulatory action is determined by a long list of characteristics that go beyond the sequence specificity of the potential binding (see Fig.1). For many of regulatory experiments, for example nucleosome positioning, ChIP-chip or ChIP-Seq peaks or DNaseI hypersensitive sites, the regulatory evidence can be converted into a prior probability over the location of potential motif sites.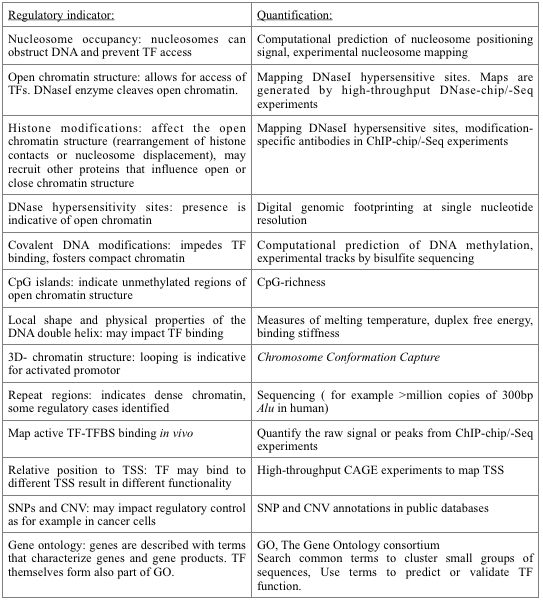
Much of such ‘new’ regulatory information, obtained from epigenetic (context-dependent) information, can be used in a discriminative way to reduce the search space in advance ('prefiltering'), or to filter out motif predictions that are not supported by the information ('post-filtering'). This 'hard' filtering approach has already shown a remarkable improvement in TFBS prediction accuracy that can be obtained from epigenetic information.

In the more 'soft' PSP approach, the search by conventional sequence-based motif detection algorithms is guided towards a more confined (so overall less noisy) space with prior regulatory evidence, at the same time not fully excluding other regions in which regulatory activity is not (or 'not yet') quantified. Using a PSP avoids the sometimes severe increase in computational complexity or runtime suffered by incorporating auxiliary information or heterogeneous data into the biological sequence model (Bailey et al., 2010).
Its elegance lays in the clean separation of introducing new regulatory information from the algorithmic motif model optimization scheme, making it quite straightforward to introduce further new, or combinations of new regulatory information into motif discovery.

Substantial progress has been made in predicting TFBSs when using PSPs constructed from nucleosome positioning (Narlikar et al., 2007), sequence conservation (Gordan et al., 2009), as also negative examples (‘discriminative’ priors) and distance to TSS (Tharakaraman et al., 2008). Also data from experimental observations such as activating and repressing histone modification marks, CpG islands, ChIP-chip and ChIP-Seq peaks, DNaseI cuts and acetylation valleys can be translated into PSPs, more than often used in a combined way to offer a maximal guidance during de novo motif detection (FIMO (Cuellar-Partida et al., 2011), CENTEPEDE (Pique-Regi et al., 2011)). A workbench as developed in PriorsEditor (Klepper and Drablos, 2013) can facilitate the creation of PSPs from different epigenetic features. This tool also allows to weigh the relative PSP contributions, as features as histone modification levels and DNasI hypersensitive locations were shown most important amongst a collection of 26 features in a human study case (GBP (Ernst et al., 2010)).

Fig.1 gives a non-exhaustive overview of some sources of regulatory information besides TF sequence specificity. Of special interest are the sources that come from experimental data as these account for particular specificities of regulation for different TFs, different tissues, different cells, different developmental stages or different organisms. Converting these measurements into a numerical value leads to a quantification of epigenetic marks on the DNA.

Impact of a PSP on the motif detection algorithm

For reasons of simplicity, we describe further how we integrated the use of a PSP in MotifSampler. The same principles have been applied for the integration of a PSP in PHMS and NOMS.

We first briefly summarize one step of the iterative Gibbs sampling scheme applied in MotifSampler for motif detection in a set of N coregulated sequences from a given species (see MotifSampler algorithm for more details):
  ...
  Update Step:
    a. select the reduced set of motif instances from the previous sampling step (= excluding the instances from a particular sequence Sz),
    b. compute the reduced motif model ~θ (= a PWM constructed by counting the nucleotide occurrences in the reduced motif instances set)
  Sampling Step:
    c. compute for each possible motif start position p in the excluded sequence Sz a predictive segment score W(p) based on the reduced motif model,
    d. sample a new motif start position in the excluded sequence Sz from the computed score-distribution W(p).
  ...
(Repeat for each sequence until the Markov chain converges)

In the standard development of our Gibbs sampling motif detection algorithms, every position in a sequence was assumed to be a priori equally likely the start of a motif. The prior distribution on the missing motif instance start positions, π(A), could hence be omitted as a constant factor in the further deviation to obtain an expression for the predictive update formula (segment score formula in step c. above). Fortunately, assuming a non-uniform prior distribution over start positions does not change the format of the predictive update formula neither impacts the final iterative Gibbs sampling scheme of our algorithms :

The values in the non-uniform prior over start positions come back as a "weight" factor that up- or downvalues the contribution of a potential DNA site in the iterative step at hand:
1) In the update step, the "weight" factor impact the construction of the reduced motif model ~θ (in step b. above). In practical terms, the PSP-based segment prior score, factorized by the PSP-impact parameter -Q, is added as a pseudocount to the nucleotide count during data-inference from the set of aligned instances in the reduced dataset. As a result, the reduced motif model ~θ will most resemble instances from the selected reduced set that have high positional prior regulatory evidence.
2) In the sampling step, before sampling takes place, the segment score distribution W(p) from step c. is combined with the non-uniform positional prior distribution on start positions in sequence Sz.

Ultimately, the impact of a non-uniform positional prior in both the update and sampling step favors the sampling of new sites in sequence Sz that occur in high-PSP regions and are similar to high-PSP segments in the other sequences of the dataset.

Using a PSP

By its definition, a PSP is a sequence of numerical non-negative values that quantifies a distinct prior regulatory belief over DNA positions. The format of the file is defined in PSP file format.

When loading a file with PSP information into our motif detectors, the prior scores on each position p, further called X(p), are internally first linearized between 0.1 and 0.9. By avoiding singularities, "zero"-scoring entries in the PSP file will less likely be visited by our motif detectors during motif search, while those positions are NOT excluded and can still be picked up as the start of a possible motif site.

Next, the linearized scores are converted into a positional prior score by the formula PSP(p) ~ X(p) ÷ (1-X(p)), representing the likelihood ratio of this position being part of a motif to this position not being part of a motif.

Finally, positional prior scores are combined into a segment prior score over length W (this value is known by the program parameter -w) and the result, PSP(a|W), is assigned to the starting position a of the candidate motif site with length W. This PSP-based prior on motif start positions is computed once for each sequence Sz before the start of the motif detection algorithm.

Special case: Create a conservation-based PSP

By defining a score that reflects the degree of sequence conservation of a DNA segment in related species (and building a PSP over DNA sequence positions from it), the use of a so-called 'conservation-based PSP' in our Gibbs sampling algorithms will favor motifs that are more likely located in cross-species conserved DNA regions over those that are not.
There are 3 advantages to this method if you want to search for well conserved motifs and exploit the principle of cross-species conservation :
1) you don't need to prealign orthologous sequences to identify conserved regions,
2) you don't necessarily need to add the orthologous sequences as input to the motif detection algorithm,
3) the score definition does not influence the complexity or runtime of the motif detection algorithm, so the user can define 'evolutionary conservation' as strict or relaxed, simple or complex as deemed acceptable.

We developed an algorithm based on suffix trees to efficiently build a conservation-based PSP file that can be used as input for our motif detectors (MotifSampler, PHMS and NOMS). The application can be run from the CreateConservationPSP webpage. To optimally run our CreateConservationPSP tool and evaluate its output, please consult the guidelines. The guidelines include more information on the formula for the computed PSP score and a link to a case study .

Feedback

Contact us if you have comments, questions or suggestions or simply want to react on the contents of this guideline. Thank you.

References

- Gordan, R., Narlikar, L., & Hartemink, A. (2009). Finding regulatory DNA motifs using alignment -free evolutionary conservation information. Nucleic Acids Research, 38(6):e90.