|
(back to : guidelines)
Demonstrate the improved motif detection performance of MotifSampler version 3.1.5 compared to version 3.1.1 on real benchmark datasets
========================================================================================================================================
The following statements are discussed in the case study :
1) weakly conserved motifs are not detectable by MotifSampler
2) weakly conserved motifs may be overshadowed by another unknown more conserved motif
3) overall good de novo motif detection when searching for mainly one instance per sequence
4) a more randomized search on different numbers of instances improves de novo detection
5) de novo searching for multiple instances per sequence requires strong overrepresentation in each sequence
6) forcing a fixed number of instances per sequence may be needed to find a motif
7) a de novo detected motif is best described when using no prior information
Conclusion
BENCHMARK SET UP
We created 43 E.coli datasets each containing 1 known motif that is described in RegulonDB (read more). The properties of the known motif in a given dataset are summarized in Table 1. The datasets differ in their number of sequences. The known biologically true motifs hidden in the different datasets differ in their degree of conservation (measured by the consensus score of the motif model available in RegulonDB) as well as in their total number of instances embedded in the dataset and their maximal number of instances per sequence in a given dataset.
In its original release, MotifSampler-3.1.1 biases the motif search towards mainly one instance per sequence. The way to derive the most likely true number of instances from the internally computed probability distribution on the number of instances in a given sequence (fig.3, Pr(x|Sk)) was done in a conservative way (an 'averaging' formula is used where the computed value in general undergoes only minor changes over the consecutive Gibbs sampling iteration steps). The current release of MotifSampler (version 3.1.5) allows more flexibility in the number of instances that are allocated in a sequence during the consecutive Gibbs sampling iterations in one run. This is done by 1) offering the choice between a wider range of prior distributions that bias the motif search in a desired direction (5 types for parameter -p) and 2) by more randomly deriving the most likely true number of instances from the distribution Pr(x|Sk) (a value is 'sampled' from Pr(x|Sk) in such way that the probability to sample X is proportional to its probability score in Pr(x|Sk)). In what follows we demonstrate the overall motif detection performance of MotifSampler-3.1.5 on the benchmark datasets and discuss why its changes upgrade the motif detection performance compared to MotifSampler-3.1.1.
DESCRIPTION OF RUNNING MOTIFSAMPLER-3.1.5
In the default setting for parameter -p (= 0.9_0.25 - prior type 1), MotifSampler-3.1.5 searches for mainly one instance per sequence. For parameter -b we select the precompiled background model of order 2 for E.coli K12 from our server, motif detection is done on the positive strand only (-s=0), we search for 1 motif (-n=1) in 100 runs (-r=100) and the motif width (-w) and maximal instances per sequence (-M) are set as known from the description of the known motif in RegulonDB. With these settings, we run MotifSampler on each of the 43 benchmark datasets mentioned above. The number of solutions reported by MotifSampler is defined as the convergence rate (Conv,**) of MotifSampler (this is not necessarily the same as the number of initiated runs (100) as some runs may be aborted and report no solution). On this list of candidate motifs, we run MotifRanking(*) to extract the different motifs that were detected by MotifSampler and to count how many times (count N) the respective motifs were detected in the given dataset. We retain as the most interesting motif from the list reported by MotifRanking : the motif with the highest LogLikelihood score that was detected at least 10 times by MotifSampler (N>10) or if not present, we retain the prediction with the yet highest motif count regardless its score.
DEFINITION OF PERFORMANCE INDICATORS
When a motif was detected (with N>10) we verify if there is enough statistical evidence for this motif to be a true one by measuring the return ratio of this motif. The return ratio of a motif (RR, **) is computed as the number of times a motif was detected (count N) divided by the number of reported solutions by MotifSampler (Conv). At the same time we verify how accurately the full set of known instances is described by the reported motif. The positive predictive value (PPV, **) is a measure for how many of the reported motif instances are true (for this we assume that instances unknown in RegulonDB are untrue) and the sensitivity (sens, **) measures how much of the known instances (as described in RegulonDB) are correctly identified in the reported set of motif instances. The best performance is obtained when PPV equals the highest value (1.00, there are no untrue instances reported) and sensitivity equals the highest value (1.00, all true instances are detected). For datasets for which no statistically significant solution was detected (all candidate motifs have N<=10), we also compute PPV and sens to verify if the solution indeed does not approximate the true motif that is known to be present in the dataset.
For each of the 43 datasets, the whole procedure (running MotifSampler and computing performance indicators) is repeated 10 times to average out
particularly good or bad results that may be obtained by chance in the stochastic framework of MotifSampler.
We report the average values of the performance indicators (Conv, RR, PPV and sens) over these 10 repetitions in a given dataset as the results of the '3.1.5-default trial'.
DESCRIPTION OF RUNNING MOTIFSAMPLER-3.1.5 WITH NON-DEFAULT SETTING FOR PARAMETER -p
Program parameter -p sets the (prior) distribution that biases the motif search towards a given number of instances in a sequence (the same prior distribution is used for every sequence in a given dataset). The default setting for parameter -p (= 0.9_0.25 - prior type 1) in MotifSampler-3.1.5 searches for mainly one instance per sequence and is used in 3.1.5-default trial. In what follows, the complete procedure of 10 times running MotifSampler and reporting averaged performance indicators (as described for 3.1.5-default trial) is repeated but each time with a different setting for parameter -p (all other program parameters described above in 3.1.5-default trial remain the same) :
'3.1.5-higher' trial : MotifSampler-3.1.5 is run with a bias to one or two instances per sequence (-p 0.9_0.75 ; prior type 1) or with a bias to mainly 2 or 3 instances per sequence (parameter -p b0.5 ; prior type 3), whichever approximates the known number of true motif instances in a given dataset best. We perform this trial only on datasets where the known motif has on average more than 1.2 known instances per sequence (Avg Load >1.2);
'3.1.5-fixed' trial : MotifSampler-3.1.5 is run without computing/updating the number of instances in each sequence during the consecutive Gibbs sampling iteration steps. The setting for parameter -p is not a 'prior' distribution, but directly fixes the exact number of instances that will be allocated in each sequence of a dataset (parameter -p f0_1 (exact 1 instance) or f0_0_1 (exact 2 instances), whichever approximates the known number of true motif instances in a given dataset best ; prior type 5) ;
'3.1.5-uniform' trial : MotifSampler-3.1.5 is run with no bias towards any particular number of instances per sequence (parameter -p u ; prior type 2, also called 'uniform' prior).
Comparing the results of 3.1.5-default trial with the results obtained in the trials where only parameter -p is changed allows evaluating the benefits of using another prior distribution on the motif detection performance.
DESCRIPTION OF RUNNING MOTIFSAMPLER-3.1.1 (previous release of MotifSampler)
To evaluate the influence of a more randomized search of different numbers of instances on the motif detection performance (i.e. 'sampling' used in version-3.1.5 instead of 'averaging' used in version-3.1.1), we internally also applied the averaging formula that was used in the earlier release of MotifSampler (version 3.1.1). To avoid influence of a biased search, we leave the setting for parameter -p equal to the uniform prior (-p u, no bias). The results of using the averaging formula combined with a uniform prior are reported as '3.1.1[mimic]-uniform' trial.
Table 2a summarizes the different trials that search for a motif in each of the 43 E. coli datasets.
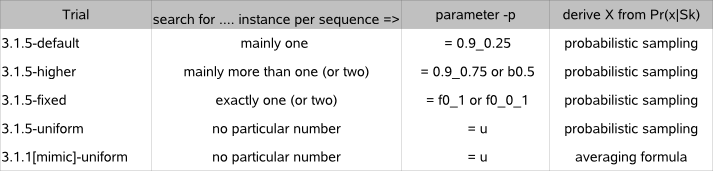
Table 2a : Different motif detection trials to evaluate the motif detection performance of MotifSampler-3.1.5
The results of each trial for each dataset are archived in Table 2.
All performance indicator results described in the following discussion are copied from or derived
(e.g. compute average value of the performance indicator over a subset of benchmark datasets) from Table 2.
1) WEAKLY CONSERVED MOTIFS ARE NOT DETECTABLE BY MOTIFSAMPLER:
The demand for a minimal degree of conservation is inherently linked to the fundaments of MotifSamplers design.
By definition, MotifSamplers algorithm searches for sets of short sequences (motifs) that are overrepresented (have a similar DNA description) compared to the surrounding nucleotides (background).
This means that biologically true motifs for which the DNA description is not significantly more conserved compared to the background DNA will not be detectable by MotifSampler (or any other overrepresentation-based motif detection algorithm).
In our case study, there are 13 (list datasets-1) out of 43 datasets for which MotifSampler did not detect a statistically significant solution in any of the trials (N is lower -or only slightly higher- than 10 in each trial). The extreme low sensitivity (order 0.1) reported for the solutions in each of these trials without significant solution confirms that almost none of the known instances was picked up in the multiple runs of MotifSampler. The conservation score of the true motif embedded in these datasets where MotifSampler could not detect any significant motif is overall low (average CS = 0.6 +/- 0.1 on a scale of 0 to 2, DgsA CS = 1.17 excluded), explaning why the motif is not detectable by MotifSampler.
The true motif in dataset DgsA, despite being well conserved, remains undetected because of the low number of true instances (4). In case of a low number of total instances, missing one true instance (because only weakly conserved) might influence the (PWM-based) motif model in MotifSampler to such extent that iteration towards the true motif is complicated.
2) WEAKLY OVERREPRESENTED MOTIFS MAY BE OVERSHADOWED BY ANOTHER UNKNOWN MORE CONSERVED MOTIF:
For another 6 (list datasets-2) of the 43 benchmark datasets, MotifSampler reports a sufficiently significant solution (N is higher than 15 in at least one trial) that however not represents the known motif as can be verified by a very low PPV and sensitivity (both order <0.1). The consensus score of these solutions is on average 20% higher than the consensus score of the known motif in RegulonDB (you can verify this in archive-table2). The higher overrepresentation of this optimum in the dataset (not necessarily representing an untrue motif) explains why MotifSampler does not find the known motif with sufficient significance in these datasets.
In addition, for 4 datasets (list datasets-3), the significance of the detected motif is moderate to high, but the proportion of detected known instances is low (sens order 0.3) and the motif is obscured by many unknown instances (PPV order 0.5). As the motif detection performance for these datasets stays at the same level in all trials, we conclude that a subset of known instances is not detectable (only very weakly conserved) and therefore overshadowed by a set of other more conserved unknown instances.
In the remaining 20 datasets (list datasets-4 and list datasets-5), MotifSampler found a solution with sufficient significance (RR>15%) that describes at least half of the known motif instances (sens>0.5) in all or at least a few trials. Unless otherwise stated, we further evaluate the sensitivity of motif detection towards different parameter settings on the number of instances per sequence on these 20 datasets.
3) OVERALL GOOD DE-NOVO MOTIF DETECTION PERFORMANCE WHEN SEARCHING FOR MAINLY ONE INSTANCE PER SEQUENCE WITH MOTIFSAMPLER-3.1.5:
When searching for mainly one instance per sequence (3.1.5-default trial) in datasets where most sequences indeed have on average one instance in each sequence (10 datasets in list datasets-4), the known motif is found with a high significance (rounded average RR = 55 +/- 25%, excluded CysB, OxyR, RutR where N<10 - these datasets are further discussed). Most of the known instances of the in general strongly conserved motif in these datasets (CS >0.8) are correctly allocated (rounded average sens = 0.85 +/- 0.10, excluded datasets CysB, OxyR, RutR) and because the prior (parameter -p) biases towards the known number of instances per sequence, almost no other (unknown) instances were picked up by the motif finder (rounded average PPV = ~0.95, excluded datasets CysB, OxyR, RutR).
When more sequences have multiple true instances (10 datasets in list datasets-5), the number of allocated instances is most likely underestimated. The 3.1.5-default trial results show that this does not prevent MotifSampler to find the true motif in these datasets and the statistical significance (rounded average RR = 70 +/- 20%, excluded NagC - this dataset is further discussed) is even higher than observed in datasets with mainly one known instance per sequence. This is not surprising as the chances to pickup a true motif in a sequence are higher if there are multiple copies of this motif in a given sequence so overall the true motif signal is easier to find. The accuracy in describing the full set of known instances is lower because of the underestimating prior (average sens = 0.55 +/- 0.10, dataset NagC excluded) which makes the motif model less accurate and more prone to also pick up a few unknown (but not necessarily untrue) instances (rounded average PPV = 0.85 +/- 0.10, dataset NagC excluded).
4) A MORE RANDOMIZED SEARCH ON DIFFERENT NUMBERS OF INSTANCES IMPROVES DE-NOVO MOTIF DETECTION
In the earlier (widely used version 3.1.1) of MotifSampler, the conservative computation ('averaging' technique) of the number of instances in a sequence performed at each Gibbs sampling step is focused on finding a true motif model (PWM), maybe at the cost of missing some true motif instances. With the upgraded more randomized way ('sampling' technique) of determining the number of instances in a sequence in the current release (version 3.1.5), the accent is more on exploring with the aim to better find the most optimal description of the full set of true motif instances. So when a sequence has one strongly conserved motif instance, the averaging technique will in general only pick up this instance, while the sampling technique may more easily also allocate two instances (e.g. when there is also a weakly conserved instance present) or no instance (when the motif model does not yet represent the true motif well). Mark that the focus on 'exploring' is less expressed towards the last iterations in a run where the random aspect is replaced by a deterministic choice of the most likely true number of instances in a sequence (convergence phase).
We observe the impact of both deviations (i.e. estimating more or less instances than exactly one) in our case study when comparing the results of 3.1.5-uniform trial (which uses sampling technique) with the results of 3.1.1[mimic]-uniform trial (which uses averaging technique) [the uniform prior excludes the inference of any external bias on the number of instances per sequence] : Allocating more than the computed average number of instances enables to pick up more of the known instances (order +0.05 to +0.10 sensitivity increase with stable PPV in the 16 datasets where the known motif was well found in all trials, list datasets-4 and -5 excluded datasets CysB, OxyR, RutR and NagC) and allocating less than the computed average number of instances results in more frequent run abortion (order +5 to +10 more aborted runs in the 16 datasets).
Once some true motif instances are picked up during the multiple iterations in a motif detection run,
the number of instances determined with the sampling technique will not differ significantly from a computed average on the number of instances,
making it unlikely that a true motif that can be found with the averaging technique will be missed when using the sampling technique.
This is indeed shown by the results on the 16 benchmark sets : the known motif is detected just as many times with both techniques.
Because of the tendency to rather abort on a run than reporting a possibly noisy solution,
the confidence in a significant solution is in general higher if obtained with sampling than with the averaging technique
(as demonstrated by a rounded average 10% increase in RR in the 16 datasets).
When the true motif is difficult to find, the more conserved approach of the averaging technique might be preferred to avoid that the convergence rate
of MotifSampler drops too low and the motif can no longer be detected with sufficient significance as is the case for datasets CysB, OxyR, RutR and NagC (Conv = ~0 respectively ~10 in sampling respectively averaging technique in these datasets).
In general however, an even more conserved approach (i.e. fixing the number of instances per sequence) will be needed to find such hard to detect motifs with sufficient significance (see below in 6) where it is shown that the known motif is only found in 3.1.5-fixed trial for sets CysB, OxyR, RutR and NagC). For this reason, we do not offer the averaging technique anymore in the current release of MotifSampler (version-3.1.5).
5) DE NOVO SEARCH FOR MULTIPLE INSTANCES PER SEQUENCE WITH MOTIFSAMPLER-3.1.5 REQUIRES STRONG OVERREPRESENTATION IN EACH SEQUENCE :
The intention of using a higher-biasing prior is to pick up multiple instances of a motif in one sequence that would be missed when searching for mainly one instance per sequence. As a result, more runs should find the motif more easily (higher RR) and the total number of true motif instances can be better approximated (higher sens). We observe this (moderately) improved detection performance in datasets DnaA, MalT, ArgR and TyrR (you can verify this in archive-table2, higher RR and/or higher PPV and sens).
A higher-biasing prior is however also more prone to pick up false instances in sequences where the motif is not present or only weakly conserved (as observed by a bit lower PPV for dataset CRP and Fur, you can verify this in archive-table2).
For most of our benchmark datasets where multiple sequences are known to have more than one instance per sequence (list datasets-5), there is no difference in performance (same order of RR, PPV and sens) when using an underestimated compared to higher-biasing prior. This demonstrates that 1) a (mildly) underestimating prior does not prevent MotifSampler to find multiple instances that are all strongly conserved in one sequence and 2) a higher-biasing prior does not necessarily improve the motif detection sensitivity if some of the true instances are only weakly conserved in one sequence.
6) FORCING A FIXED NUMBER OF INSTANCES PER SEQUENCE MAY BE NEEDED TO FIND THE MOST OVERREPRESENTED SIGNAL IN A DATASET
(we discuss here datasets CysB, OxyR, RutR and NagC excluded in the earlier discussions)
For some datasets only a subset of the initiated runs reports a solution (we consider that this did not occur by chance if Conv <70). By design, run abortion happens because at some point in the consecutive iterations only 2 or less instances are allocated in the dataset. Obviously, the chances this happens are higher when the number of sequences in a dataset is low as observed for dataset RutR that consists of only 4 sequences (with each one known instance) where a motif could not be detected in 3.1.5-default trial despite its reasonably well conserved true motif (motif CS = 1.17). When moreover the true motif is well conserved in a few sequences only (and not or only very weakly conserved in the other sequences of the dataset), the chances no instances are picked up in most sequences of a small dataset are significantly high, as observed for datasets CysB, OxyR and NagC (size dataset <10 sequences, motif CS <0.8, Conv <40). Motif detection results obtained at low convergence rate are 1) not suitable for the assessment of motif significance and 2) indicate that the motif is difficult to find in the dataset.
The most critical phase for run abortion is the early stage of Gibbs sampling iterations where for the first time no instances may be allocated in a sequence and where the motif model may not (yet) approximate an overrepresented signal well. When MotifSampler-3.1.5 is forced to allocate exactly one instance per sequence at this stage, run abortion will not occur enabling the motif finder to yet further explore the solution space and find the (more difficult to find) motif after all. For datasets CysB, OxyR, RutR and NagC, the motif is then detected with a sufficiently high statistical significance (RR>15%) and with a high number of true motif allocations (sens order 0.75, for CysB sens 0.55) with only a limited fraction of unknown (not necessarily untrue) instances (PPV order 0.75) (you can verify the 3.1.5-fixed trail results in archive-table2).
In de novo motif detection, it is in general better not to allocate an instance in a sequence than to allocate a false instance, explaining why we do not set the search to exactly one (or two) instances per sequence as a default in MotifSampler-3.1.5. The motif description in the 16 datasets where the known motif is well detected in all trials is indeed not better (PPV and/or sens are lower or same) when MotifSampler 'forces' instead of 'guides' the allocation towards 1 or 2 instances per sequence (you can verify this in archive-table2 by comparing the results of 3.1.5-fixed trial with 3.1.5-default [or 3.1.5-higher, whichever is best] trial in list datasets-4 and -5, excluded datasets CysB, OxyR, RutR and NagC).
7) A DE NOVO DETECTED STATISTICALLY RELEVANT MOTIF IS BEST DESCRIBED WHEN USING NO PRIOR INFORMATION (-p = uniform prior)
In general, the number of instances in the different sequences of a dataset varies from zero (for noisy sequences) to multiple instances (for sequences with high coregulatory evidence). So even if a true motif signal is well detected when using a biasing prior (that applies to every sequence in the dataset), the number of instances will be over- or underestimated in at least some sequences of the dataset. This is not the case when MotifSampler is run without applying any bias towards a particular number of instances per sequence. If a significant solution is found, the number of instances is only driven by the motif signal itself. The description of the full set of known instances in each of the 16 datasets where the known motif signal is well detected in all trials is indeed equal to or slightly better (PPV and/or sens) than the best description reported in any of the earlier discussed trials (you can verify this in archive-table2).
Also the fraction of solutions that reports a noisy motif (not reflecting an overrepresented signal) will be lower when there is no biasing information that may deviate the motif search away from a true motif, as demonstrated by a very high return ratio (rounded average RR 80% +/ 15% over the 16 datasets in 3.1.5-uniform trial - and RR in each dataset is always higher than RR in 3.1.5-default or 3.1.5-higher trial, you can verify this in archive-table2). On the other hand, when the motif model does not (yet) approximate a (true or untrue) overrepresented signal at early stage of Gibbs sampling iterations in a run, chances are high that too few instances will be allocated (as there is no guidance to pickup at least some instances) and the run gets aborted. In the 16 datasets we indeed observe a moderate convergence rate (on average 60 +/- 20 non-aborted runs compared to ~90-100 non-aborted runs in the earlier discussed trials), but the number of solutions where the known motif was detected is still very high (order more than 30 and almost equally high as in 3.1.5-default or 3.1.5-higher trial) demonstrating that a solution with high return ratio despite low convergence rate can still be regarded as a likely true motif prediction.
If the motif signal is not very strongly conserved in a dataset, run abortion will occur too frequently as observed for datasets CysB, OxyR, RutR and NagC (Conv<10) degrading the confidence level for a user that a solution would represent a true motif (although this may be well true as observed for dataset RutR where 3 out of 3 runs report 3 out of 4 known instances (sens 0.75) and no unknown allocations (PPV=1.00)).
CONCLUSION
The current release of MotifSampler (version-3.1.5) shows a better motif detection performance compared to our widely used well performing version 3.1.1. If a motif is detectable, the default search for mainly one instance per sequence will find the core of a motif well and if a motif is not (or weakly) detectable, it will rather report no solution than a noisy solution. Offering the possibility to search for a fixed number of instances per sequence enables to detect weakly overrepresented motifs in a dataset. Offering the possibility for no bias towards any number of instances per sequence allows finding the most optimal representation of a motif in a dataset. If one wants to be sure all instances have been detected we advise to run a motifscreening (MotifLocator) with a strict motif model to pick up the missing instances, rather than exploring prior distributions that bias towards multiple instances of a motif per sequence. Using an overestimated prior might result in a motif prediction that deviates too much from the true underlying motif signal and will only be beneficial (it will give a more complete description of all true instances) when you have firm evidence that most sequences in a dataset indeed have a more or less equal higher (2 or 3) instances per sequence.
LIST DATASETS (the motif detection results for these datasets can be consulted in archive table2) :
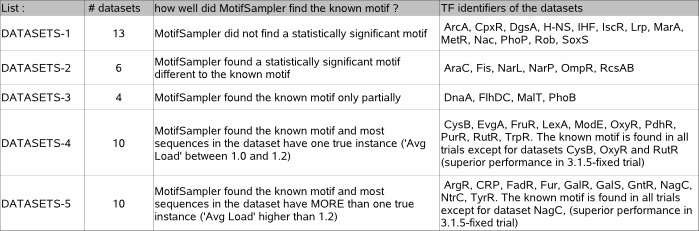
Each of the 43 datasets is added to one list depending on how well the known motif was found by MotifSampler in this dataset. Datasets in list-4 and list-5 differ in the average number of known true instances per sequence of the dataset ('Avg Load' data in table 1).
Bookmarks:
-----------------------------
(*) See Running MotifSuite on the benchmark datasets for the parameter settings used in MotifRanking and MotifComparison.
(**) See Computation of performance indicators for definitions on Conv, N, RR, PPV, sens.
|



