|
(back to : guidelines)
Demonstrate the added value of constructing ensemble motifs using FuzzyClustering on real benchmark datasets.
==========================================================================================================
The following statements are discussed in the case study :
1) detection frequency indicators (Occ(i) and N(m)) allow filtering spurious solutions
2) constructing an ensemble motif allows exceeding the quality of the best motif predicted by a single run of MotifSampler
3) the coherence of the instance memberships in an ensemble motif is an indicator for the accuracy with which a motif can be predicted
4) the benefits of a conserved representation offered by an ensemble PWM
Conclusion
BENCHMARK SET UP
We created 43 E. coli datasets each containing one known motif (taken from RegulonDB, read more).
We ran MotifSampler(*) 100 times on each dataset and reported the convergence rate (Conv), that is the total number of solutions (motifs) reported by these 100 stochastically initiated motif detection runs.
In what follows, we demonstrate the added value of constructing ensemble motifs (filtering false predictions, picking up weakly conserved motifs, obtaining informative PWMs) and how to interprete different indicators of an ensemble motif (Occ(i) and dM(i), defined further).
DESCRIPTION OF RUNNING FUZZYCLUSTERING
We ran FuzzyClustering on the list of motifs reported by multiple runs of MotifSampler (each motif is described by a set of instances) for a given
sequence set (each of the benchmark 43 datasets) with the following parameter settings.
Instances that occur in less than 10% of the supplied motifs are removed from the input to FuzzyClustering as being spurious (unreliable) predictions
(prefiltering parameter -p = 0.1). The fractional threshold below which instances and motifs extracted by FuzzyClustering are considered as unreliable
and as consequence are removed from an extracted cluster is computed by the program (parameter -m = default no input).
Only ensemble motifs that occur in at least 50% of the sequences (parameter -i = 0.5), that are supported by at least 20% of the supplied motifs
(parameter -j = 0.2) and that have a PWM consensus score higher than 0.25 (parameter -c) are reported in the output.
PRIORITIZE THE MOST LIKELY TRUE MOTIFS
>From the list of ensemble motifs reported by FuzzyClustering, we select the one with the highest instances weighted_average_occurrence
(Occ(i), an indicator for the detection frequency of the ensemble motif instances in the sequence set by MotifSampler), further called (ensemble) motif-1. If the list contains another motif with Occ(i) >10, we select this prediction as (ensemble) motif-2.
DEFINITION OF PERFORMANCE INDICATORS
For each motif-1 and (if present) motif-2, we report the indicators Occ(i), N(m) and CS which are explicitly available in the output of FuzzyClustering.
The instances weighted_average_occurrence (Occ(i), **) is an indicator for the number of times (an instance of) the ensemble motif was (on average)
detected by the multiple runs in MotifSampler. The weighted motif count (N(m), **) is an indicator for the number of de-novo detected motifs by
MotifSampler that support the ensemble motif (i.e. correspond to the same motif as the ensemble motif). The consensus score (CS)
of the motif's PWM representative reflects the conservation of the ensemble motif. We also report the difference between the maximal and minimal
membership score (dM(i) = delta instance membership) to evaluate how coherently the eventual instances represent the ensemble motif.
Finally, we verify how accurately the full set of known instances in our benchmark is covered by the instances of the ensemble motif.
The positive predictive value (PPV, **)
is a measure for how many of the ensemble instances are true (for this we assume that instances unknown in RegulonDB are untrue) and
the sensitivity (sens, **) measures how many of the known instances (as described in RegulonDB) are correctly identified in the ensemble instances. The best performance is obtained when PPV equals the highest value (1.00, there are no untrue instances reported) and sensitivity equals the highest value (1.00, all true instances are detected).
For each of the 43 datasets, MotifSampler was repeated 10 times to average out particularly good or bad results that may be obtained
by chance in the stochastic framework of MotifSampler. So here we run the whole procedure (running FuzzyClustering and computing performance indicators) on each of the 10 MotifSampler outputs on a given dataset.
We report the average values of the performance indicators (Occ(i), N(m), dM(i), CS, PPV and sens) over these 10 repetitions in a given dataset in
Table 4. All performance indicator results described in the following discussion are copied or derived
(e.g. compute an average value of the performance indicator over a subset of benchmark datasets) from Table 4.
1) DETECTION FREQUENCY INDICATORS (Occ(i) and N(m)) ALLOW SUCCESFULLY FILTERING SPURIOUS SOLUTIONS
Spurious solutions do not reflect an overrepresented motif signal and are removed from the output by FuzzyClustering in several filtering steps.
The parameter settings in FuzzyClustering that influence the balance between filtering out such spurious solutions while still retaining biologically
true motifs that are difficult to detect have been empirically set so that an ensemble motif 1) (parameter -p:) does not contain randomly detected
instances (that occur less than 10 times in 100 MotifSampler runs), 2) (parameter -m:) does not consist of instances and corresponding motifs
(detected by MotifSampler) that only weakly (relative low membership score) contribute to the ensemble motif, 3) (parameter -i:) occurs in a sufficient
fraction (more than 50%) of the sequences, 4) (parameter -j:) is supported by a sufficient fraction (more than 20%) of the MotifSampler runs and
5) (parameter -c:) is sufficiently conserved (PWM consensus score higher than 0.5).
For 11 out of 43 datasets (datasets list-1a), FuzzyClustering reports no solution that meets all these criteria so no significant ensemble motif is
reported in those cases. Solutions obtained at less stringent post processing parameter settings (-j 0.1 or -c 0.25) in these datasets indeed hardly
correspond to the known motif (sensitivity <0.3) and consist mainly of unknown instances (PPV <0.3).
For a weakly overrepresented motif in a sequence set, many MotifSampler runs may detect some of the (difficult to detect) true motif instances
while most of the true motif instances are only detected in a limited number of MotifSampler runs (meaning that
different MotifSampler runs each time detect a different subset of the true motif instances interfered with other instances that do not belong to
the respective motif). An ensemble motif extracted from such a set of interfered MotifSampler motifs can therefore be identified by comparing the number of
times its instances were on average detected in the multiple runs of MotifSampler (measured by the weighted average instances occurrence, Occ(i))
with the number of MotifSampler runs that contributed to the formation of the ensemble motif (measured by N(m)). From our experience, ensemble motifs for which the instances were detected at a moderate frequency (Occ(i) is lower than 30 on 100 reported solutions of
MotifSampler) despite the fact that the motif is well supported by the input data (N(m) is at least order 10 higher than Occ(i)), do not reflect a
distinct overrepresented motif signal and are best removed from the output. Such an obscured ensemble motif (Occ(i) =~ 30 while N(m) =~ 50) was reported for 3 out of 43 datasets (datasets list-1b). The decision to not retain
these predictions seemed correct as the ensemble motif hardly corresponds to the known motif (sensitivity<0.3) and consisted mainly of unknown
instances (PPV<0.2).
In all these 14 datasets for which eventually no ensemble motif was retained, the low overrepresentation of the known motif
complicated its de novo detection as shown by: 1) its weak conservation (consensus score lower than 0.8) and 2) the most
significant motif predicted by MotifSampler (MotifRanking is used to select this motif, see results in
Table 3) does not represent the known motif.
2) CONSTRUCTING AN ENSEMBLE MOTIF ALLOWS TO EXCEED THE QUALITY OF THE BEST MOTIF PREDICTION BY MOTIFSAMPLER
Amongst the motifs reported by multiple runs of MotifSampler, the best prediction is the motif with the highest motif score amongst a sufficiently
large set of detected motifs that all describe the same motif (MotifRanking is used to select this motif). As the true motif properties (e.g. the
number of instances in each sequence) are unknown to MotifSampler, even the best motif might contain spurious annotations or may miss true instances
that were detected in other runs of MotifSampler. A clustering approach as used in FuzzyClustering aims to extract all and only true instances by
evaluating the MotifSampler results at their instance level, eventually resulting in an ensemble motif that exceeds the quality of all the individual
motifs reported by MotifSampler.
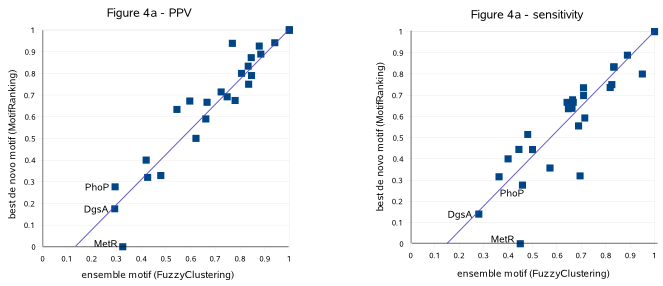
Fig. 4a shows the PPV (left) and sensitivity (right) of the ensemble motif constructed by FuzzyClustering (X-axis, results extracted from archive-Table 4)
compared with the quality of the best motif (selected by running MotifRanking on the motif predictions by 100 runs) of MotifSampler (Y-axis, results extracted from MotifRanking archive-Table 3)
in 28 benchmark datasets (datasets list-2[Rob excluded]). The correlation lines demonstrate that the ensemble motif consists of
more true instances (higher sensitivity) and less unknown instances (higher PPV) for datasets in which the known motif is not well described by the best
MotifSampler/MotifRanking motif (PPV or sensitivity <0.8, in the other cases both motifs describe the known motif equally well as shown by a
same high PPV and sensitivity). Mark that FuzzyClustering could even (partially) retrieve the known motif in datasets DgsA, MetR and PhoP
for which the de novo detection was strongly interfered by unknown instances (no significant motif was retained from the MotifSampler/MotifRanking
results in these datasets).
3) THE COHERENCE OF THE INSTANCE MEMBERSHIPS IS AN INDICATOR FOR THE ACCURACY WITH WHICH A MOTIF CAN BE PREDICTED
The instance memberships are scores that prioritize how well each instance represents the ensemble motif compared to the other instances of this motif.
All ensemble instances having about the same score indicates that all these instances were detected equally coherent in multiple runs of MotifSampler
and that false annotations (if so present in these runs) were filtered out when constructing the ensemble motif.
Observing a high difference between the maximum and minimum reported instance membership in an ensemble motif (dM(i)) indicates there were
interfering instances during de novo motif detection. dM(i) correlates well with the degree of false annotations (PPV) that could not be
filtered from the ensemble motif (Fig. 4b):
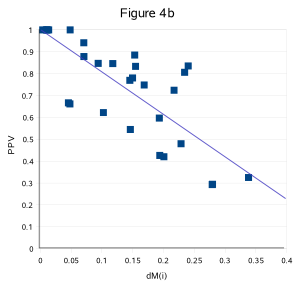
Fig. 4b shows the delta between the extreme instance memberships (dM(i)) and the positive predictive value (PPV) of the ensemble motif (motif-1)
in 28 benchmark datasets (datasets list-2[Rob excluded], dM(i) and PPV extracted from archive-Table 4/list-2).
Ensemble motifs consisting of a set of coherently detected instances (in the range dM(i)<0.15) are hardly interfered by unknown instances
(PPV is high, order 0.8-1) while more unknown instances are present (lower PPV) in ensemble motifs for which the instance memberships have more
extreme values (higher dM(i)).
Repeating FuzzyClustering with an external setting for parameter -m (higher than the internally computed membership cutoff threshold reported by
%InstanceCut) will return a more accurate ensemble motif (less reliable instances are further removed and dM(i) will decrease).
In general however, this will be at the cost of also removing true instances.
For all except 5 (out of 28) benchmark datasets, we could conclude that known motif was best described by the ensemble motif obtained in the default
FuzzyClustering run (the membership scores of the known and unknown ensemble instances were of the same order (data not shown)
so using a higher fractional membership cutoff would remove too much instances and a lower cutoff would also include unknown instances).
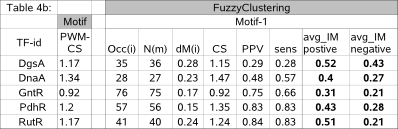
Table 4b shows the average instance membership score (avg_IM) of the ensemble instances that are known (positive) and of the
ensemble instances that are unknown (negative, assumed to be untrue) for the 5 excluded datasets
(Table 4b, other indicators are extracted from archive-Table 4). The gain in accuracy by using a more stringent instance membership cutoff
is expected to be minor because the accuracy of the current ensemble motif is already high (PPV order 0.8) or (for DgsA and DnaA,
which consist of 5 respectively 7 instances) the total number of ensemble instances is low (so it concerns the removal of only one instance),
supporting our recommendation that leaving the parameter -m at default value is usually a good choice.
4) THE BENEFITS OF A CONSERVED REPRESENTATION OFFERED BY AN ENSEMBLE PWM
Instances of a motif that mutually resemble each other most (conserved instances) in general have a relative high instance membership score
(as they are more easy to detect) and contribute more to an ensemble PWM (*) than the less conserved instances of the motif.
As a result, ensemble PWMs tend to reflect mainly the conserved core of the true motif.
Fig. 4c shows the PWM consensus score of the known motif (known-CS) and the consensus score of the ensemble PWM (ensemble-CS)
in 28 benchmark datasets (datasets list-2[Rob excluded], CS extracted from archive-Table 4/list-2) :
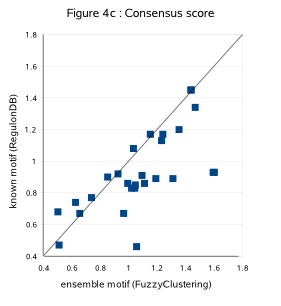
When the known motif is strongly conserved (known-CS > 1), its instances are easily detected (all have equally high membership scores)
and the ensemble PWM reflects the same degree of conservation as the known PWM (same CS).
For less conserved true motifs (known-CS < 1), the less conserved instances contribute less to the ensemble PWM than the well conserved ones
and the consensus score of the ensemble motif is in general higher compared to the consensus score of the known benchmark motif.
Benefits:
- Ensemble motifs with a very low consensus score (lower than parameter -c) are not reported by FuzzyClustering.
As a first benefit, the overestimated ensemble PWM consensus score allows FuzzyClustering to still report ensemble motifs that consist of at
least a subset (the more conserved instances) of a difficult to detect motif, as observed for 3 datasets in our benchmark (Table 4d):
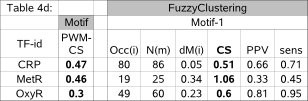
Table 4d shows the indicators of an ensemble motif (Occ(i), N(m), PPV, sensitivity and consensus score) in 3 datasets where the known motif is
very difficult to detect (as indicated by their very low consensus score).
By focusing on mainly the conserved instances, the ensemble motif is significant (Occ(i) is high or of the same order as N(m))
and passed the PWM consensus score filter (CS > 0.5).
- Many motif evaluation tools are PWM-based: the PWM representation of a given motif is used in genome-wide scanning of DNA sequences for instances of
this motif (as done in MotifLocator**) or the PWMs of two motifs are compared to judge their similarity (as used in MotifComparison** and
MotifRanking**). When a given motif is only weakly conserved, its PWM representation is uninformative (many positions have equal weights for
A,C,G and T) and the PWM-based motif evaluation tools lose their selectivity (too much false annotations in genome-wide scanning and too much motifs
are found similar because of many equally uninformative positions). The use of a more conserved motif representation (as obtained with FuzzyClustering)
of such weakly conserved motifs can increase the selectivity of such PWM-based motif evaluation tools.
(*) An 'ensemble PWM' stands for the PWM representative constructed from the alignment of all instances of the ensemble motif. The contribution of each instance in the PWM is proportional with its membership score in the ensemble motif.
(**) MotifLocator, MotifComparison and MotifRanking are motif evaluation tools available in MotifSuite.
CONCLUSION
When FuzzyClustering does not report a consistently detected ensemble motif (i.e. Occ(i)>30 if not Occ(i) =~ N(m)) for a given dataset
(even when repeating MotifSampler with different parameter settings that further explore the motif solution space),
one should conclude that the true motif (if so present) is not easily detectable by de novo motif detection.
The ensemble motifs obtained at default parameter settings are in general good descriptions of a true motif that equal or exceed the accuracy of the
best de novo detected predictions obtained by multiple MotifSampler runs (summarized with MotifRanking).
Repeating FuzzyClustering with an external (more stringent) instance membership cutoff (parameter -m) is advised when the instance membership scores
in an ensemble motif mutually differ largely (high dM(i)): as long as the detection frequency indicators (Occ(i) and N(m)) are of the same order
as in the default run, the ensemble motif obtained in the second attempt describes the true motif more accurate.
If different ensemble motifs are reported, FuzzyClusterings metrics (Occ(i), N(m), dM(i) and CS-score, in that order) can be used to prioritize the detected motifs.
LIST DATASETS (the FuzzyClustering results for these datasets can be consulted in archive Table 4) :

Each of the 43 datasets is added to one list depending if an ensemble motif was retained or not.
Bookmarks:
-----------------------------
(*) See Running MotifSuite on the benchmark datasets for the parameter settings used in MotifSampler.
(**) See Computation of performance indicators for definitions on Conv, Occ(i), N(m), PPV, sens.
|







