Multithreaded Computation

Many MATLAB functions support multithreaded computation, providing improved performance on multicore and multiprocessor systems. These functions include linear algebra operations that call the BLAS library (e.g. matrix multiply, QR decomposition) and element-wise numerical operations (e.g. sin, log). This example shows the performance improvement for multiple functions on a dual-core system using two computational threads.

Contents

Configuring Multithreaded Computation via the Preferences Panel

To enable multithreaded computation, select File > Preferences > General > Multithreading and select Enable multithreaded computation as shown here:

For optimal performance, it is recommended that you accept the default for Maximum number of computational threads, which is Automatic.

About the Helper Function Used in this Demo

To illustrate performance improvement for multiple functions, this demo uses the helper function runAndTimeOps. This helper function is undocumented and unsupported at this time.

Measuring Performance Improvement for a Single Operation

This example uses two threads (defined in the variable numThreads) for one sample operation, matrix multiply. You can experiment by increasing the number of threads if your system has more than two CPUs. There are some overhead costs associated with running code the first time, so perform timing comparisons with a second and subsequent runs to remove effects of that overhead.

First, define some parameters and generate random data in variables A and B.

numThreads=2;              % Number of threads to test
dataSize=500;              % Data size to test
A=rand(dataSize,dataSize); % Random square matrix
B=rand(dataSize,dataSize); % Random square matrix

Next, set the number of computational threads to one and time the operation of interest.

oldstate = maxNumCompThreads(1);
C=A*B;       % Do not perform timing comparison with the first run
tic;
C=A*B;
time1=toc;
fprintf('Time for 1 thread  = %3.3f sec\n', time1);

Time for 1 thread  = 0.035 sec

Now, set the number of computational threads to numThreads and time the operation. You can experiment by increasing the number of threads if your system has more than two CPUs.

maxNumCompThreads(numThreads);
tic;
C=A*B;
timeN=toc;
fprintf('Time for %d threads = %3.3f sec\n', numThreads, timeN);

Time for 2 threads = 0.020 sec

Calculate performance improvement.

speedup=time1/timeN;
fprintf('Speed-up is %3.3f\n',speedup);

Speed-up is 1.714

Measuring Performance Improvement for Multiple Operations

This example illustrates performance improvements for multiple functions. It uses the helper function runAndTimeOps to compute the average of a few runs. First, look at the helper function:

type runAndTimeOps

function [meanTime names] = runAndTimeOps
% Time a number of operations and return the times plus their names.
% Other functions can be inserted here by replicating the code sections.

% Set parameters
numRuns = 10;               % Number of runs to average over
dataSize = 500;             % Data size to test
x=rand(dataSize,dataSize);  % Random square matrix

% Matrix multiplication (*)
func=1; % Initialize function counter
tic;
for i = 1:numRuns
    y=x*x;                  % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='*';            % Store string describing function
func=func+1;                % Increment function counter

% Matrix divide (\)
tic;
for i = 1:numRuns
    y=x\x(:,1);             % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='\';            % Store string describing function
func=func+1;                % Increment function counter

% QR decomposition
tic;
for i = 1:numRuns
    y=qr(x);                % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='qr';           % Store string describing function
func=func+1;                % Increment function counter

% LU decomposition
tic;
for i = 1:numRuns
    y=lu(x);                % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='lu';           % Store string describing function
func=func+1;                % Increment function counter

% Sine of argument in radians
tic;
for i = 1:numRuns
    y=sin(x);               % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='sin';          % Store string describing function
func=func+1;                % Increment function counter

% Array power
tic;
for i = 1:numRuns
    y=x.^x;                 % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='.^';           % Store string describing function
func=func+1;                % Increment function counter

% Square root
for i = 1:numRuns
    y=sqrt(x);              % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='sqrt';         % Store string describing function
func=func+1;                % Increment function counter

% Element-wise multiplication (.*)
tic;
for i = 1:numRuns
    y=x.*x;                 % Call function
end
meanTime(func)=toc/numRuns; % Divide time by number of runs
names{func}='.*';           % Store string describing function
func=func+1;                % Increment function counter

Now call the function. Set the number of computational threads to one and time the operations.

maxNumCompThreads(1);         % Set number of threads
[time1thread functionNames]=runAndTimeOps;  % Time operations

Set the number of computational threads to numThreads and time the operations again.

maxNumCompThreads(numThreads); % Set number of threads
[timeNthreads functionNames]=runAndTimeOps;  % Time operations

Restore the number of computational threads to the setting before the demo.

maxNumCompThreads(oldstate);

Calculate performance improvements.

speedup=time1thread./timeNthreads;    % Speed-up for all functions

Plotting the Performance Improvements for the Operations

bar(speedup); % Plot speed-up for all operations as bar chart
title(['Performance Improvement with ' int2str(numThreads) ' Threads on Arrays of ' int2str(dataSize) 'x' int2str(dataSize)]);
ylabel('Performance Improvement');
set(gca, 'XTickLabel', functionNames);
ylim([0 2.25]); % Set Y axes to fixed max value
xlim([0 length(functionNames) + 1]); % Set X axes to fixed max value
grid;

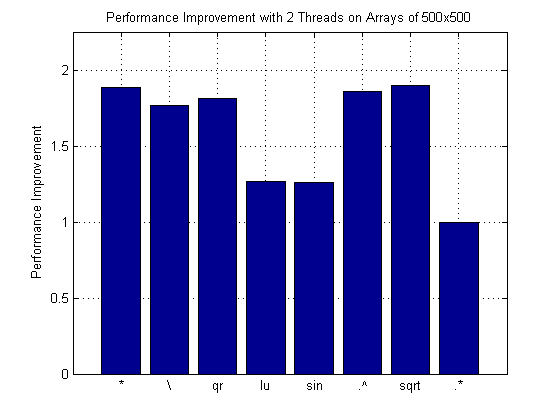
Analyzing Performance Results and Other Issues

As shown, not all functions benefit from multithreaded computation. For example, simple element-wise multiplication does not because it is a memory-bound operation. For functions that benefit, performance gains on multicore and multiprocessor systems vary with data set size. You can experiment with the data set size in this example, or even plot improvements against data set size.

Note that element-wise operations do not run faster when used in debugging or publishing. This is because element-wise multithreaded computation is provided by the JIT/accelerator, which is not used in these situations.

Disabling Multithreaded Computation

If you do not want to use multithreaded computation, disable it via Preferences.

Copyright 1984-2007 The MathWorks, Inc.
Published with MATLAB® 7.7

MATLAB and Simulink are registered trademarks of The MathWorks, Inc. Please see www.mathworks.com/trademarks for a list of other trademarks owned by The MathWorks, Inc. Other product or brand names are trademarks or registered trademarks of their respective owners.