Function Functions

In MATLAB®, one function take another as a parameter. This feature serves a wide variety of purposes. Here we illustrate its use for finding zeros, optimization, and integration.

The HUMPS Function
Plot of HUMPS
Zero of HUMPS
Minimum of HUMPS
Integral of HUMPS

The HUMPS Function

A MATLAB function is an M-file that starts with the keyword function. This is what the function HUMPS looks like:

type humps

function [out1,out2] = humps(x)
%HUMPS  A function used by QUADDEMO, ZERODEMO and FPLOTDEMO.
%   Y = HUMPS(X) is a function with strong maxima near x = .3 
%   and x = .9.  
%
%   [X,Y] = HUMPS(X) also returns X.  With no input arguments,
%   HUMPS uses X = 0:.05:1.
%
%   Example:
%      plot(humps)
%
%   See QUADDEMO, ZERODEMO and FPLOTDEMO.

%   Copyright 1984-2002 The MathWorks, Inc. 
%   $Revision: 5.8 $  $Date: 2002/04/15 03:34:07 $

if nargin==0, x = 0:.05:1; end

y = 1 ./ ((x-.3).^2 + .01) + 1 ./ ((x-.9).^2 + .04) - 6;

if nargout==2, 
  out1 = x; out2 = y; 
else 
  out1 = y;
end

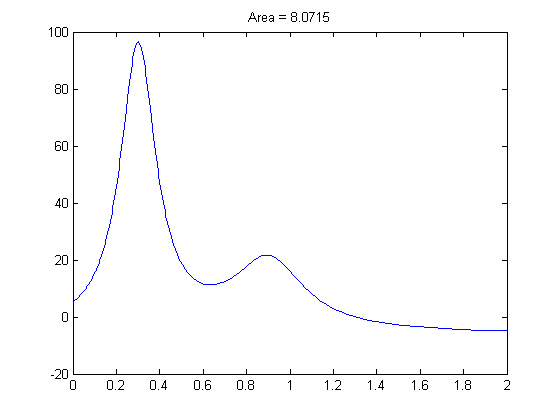
Plot of HUMPS

This figure shows a plot of HUMPS in the domain [0,2] using FPLOT.

fplot(@humps,[0,2]);

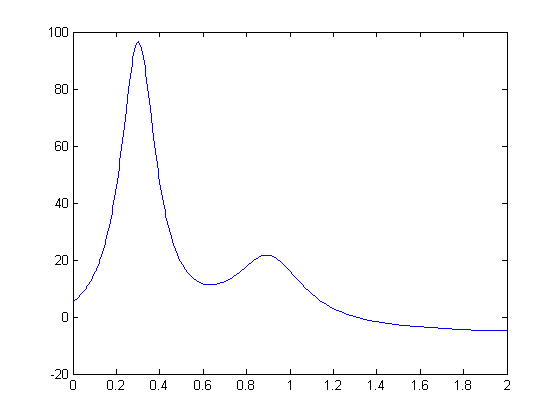
Zero of HUMPS

The FZERO function finds a zeros of a function near an initial estimate. Our guess here for HUMPS is 1.

z = fzero(@humps,1,optimset('Display','off'));
fplot(@humps,[0,2]);
hold on;
plot(z,0,'r*');
hold off

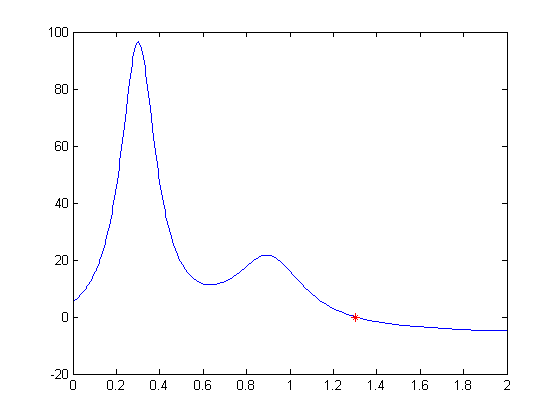
Minimum of HUMPS

FMINBND finds the minimum of a function in a given domain. Here, we search for a minimum for HUMPS in the domain (0.25,1).

m = fminbnd(@humps,0.25,1,optimset('Display','off'));
fplot(@humps,[0 2]);
hold on;
plot(m,humps(m),'r*');
hold off

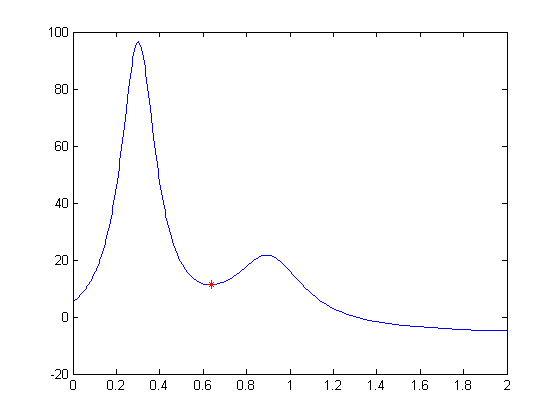
Integral of HUMPS

QUAD finds the definite integral of HUMPS in a given domain. Here it computes the area in the domain [0.5, 1].

q = quad(@humps,0.5,1);
fplot(@humps,[0,2]);
title(['Area = ',num2str(q)]);